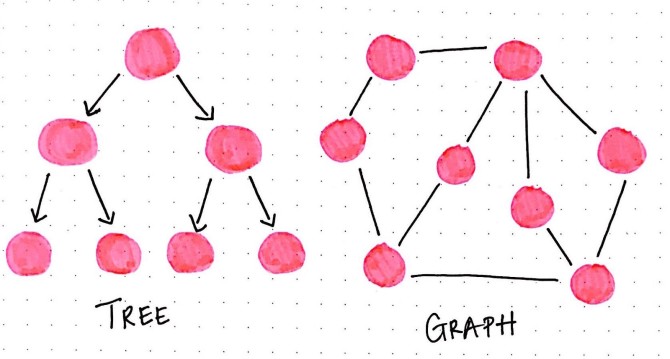
Trees start from a root node and might connect to other nodes, which means that could contain subtrees within them. Trees are defined by a certain set of rules: one root node may or may not connect to others, but ultimately, it all stems from one specific place. The tree follows one direction and cannot have loops or cyclical links.
Graphs are non linear structures: their data doesn’t follow an order. Trees will always be graphs, but not all graphs will be trees. Graphs do not have a concept of a root node. They can have a direction or not or they could have some links that have direction and others that don’t. Every graph must have at least one single node. (a graph with one node is called singleton).
Edges (sometimes referred to as links) can connect nodes in any way possible. Edges are what differentiates graphs. There are two types of edges: a edge that has a direction or flow, and an edge that has no direction or flow. We refer to these as directed and undirected edges, respectfully. In a directed edge, we can only travel from the origin to the destination, and never the other way around (digraph). However, it’s an entirely different story with undirected edges. In an undirected edge, the path that we can travel goes both ways. That is to say, the path between the two nodes is bidirectional, meaning that the origin and destination nodes are not fixed.
In mathematics, graphs are a way to formally represent a network, which is basically just a collection of objects that are all interconnected. For example, in mathematical terms, we describe graphs as ordered pairs. Remember high school algebra, when we learned about (x,y) ordered pair coordinates? Similar deal here, with one difference: instead of x and y, the parts of a graph instead are: v, for vertices, and e, for its edges. If our graph has more than one node and more than one edge that ordered pair — (V, E) — is actually made up of two objects: a set of vertices, and a set of edges. The “unordered†part is really important here, because remember, unlike trees, there is no hierarchy of nodes.
Facebook, a massive social network, is a type of graph. Twitter, on the other hand, works very differently from Facebook. I can follow you, but you might not follow me back.
References+Image
Vaidehi Joshi, A Gentle Introduction To Graph Theory. In Medium, Retrieved from here